Circumcenter of a triangle
Intro
It’s useful to sometimes redo high school basic stuff step by step. Also I wanted to try out the mathjax latex embedding.
This article also features zero production quality diagrams made in paint which I really like because it’s fast.
Definition
A circumcenter of a triangle (A, B, C) is a point P that is equally distant to 3 of its vertices.
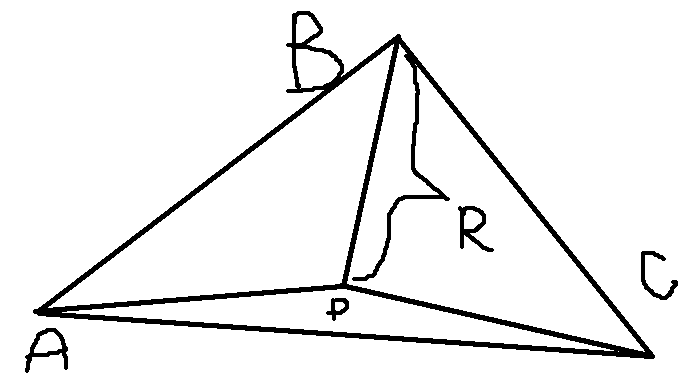
Or it’s an intersection point between 3 perpendicular bisectors(rays that divide an edge in two equal halves and are perpendicular to that edge).
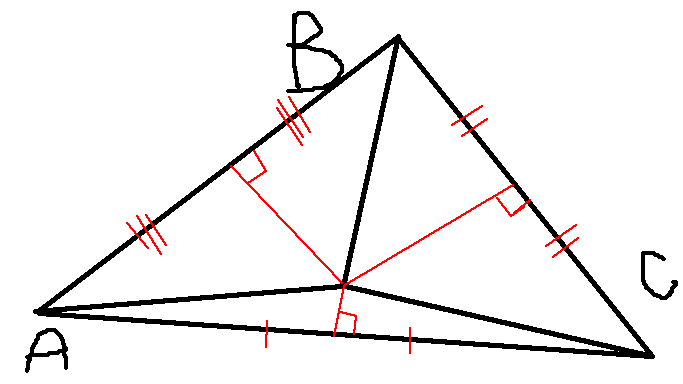
Solution
One way to find the circumcenter is to find the intersection between two bisectors, for example, for edges AB and AC. This works because the bisector of an edge is a set of equidistant points from its vertices, so intersection of two bisectors is a point that is equidistant to 3 vertices. We do that by solving the equation:
\[P = AB + AB_{\bot } * t_0 \\ P = AC + AC_{\bot } * t_1\]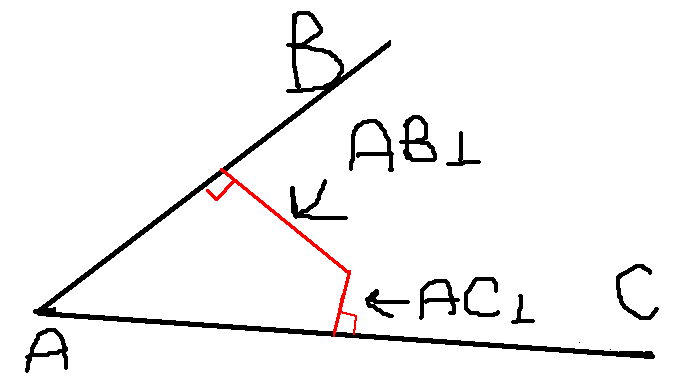
Where:
Centers of edges:
\[AB_x = \dfrac{A_x + B_x}{2} \\ AB_y = \dfrac{A_y + B_y}{2} \\ AC_x = \dfrac{A_x + C_x}{2} \\ AC_y = \dfrac{A_y + C_y}{2} \\\]Perpendicular bisectors of edges:
\[AB_{\bot x} = A_y - B_y \\ AB_{\bot y} = B_x - A_x \\ AC_{\bot x} = A_y - C_y \\ AC_{\bot y} = C_x - A_x \\\]Which just says that two rays arrive at some point P. If we expand each dimension:
\[P_x = AB_x + AB_{\bot x} * t_0 \\ P_y = AB_y + AB_{\bot y} * t_0 \\ P_x = AC_x + AC_{\bot x} * t_1 \\ P_y = AC_y + AC_{\bot y} * t_1 \\\]We have 4 variables and 4 equations. MATRIX TIME!!!11
\[\begin{bmatrix} P_x \\ P_y \\ P_x \\ P_y \\ \end{bmatrix} = \begin{bmatrix} AB_x + AB_{\bot x} * t_0 \\ AB_y + AB_{\bot y} * t_0 \\ AC_x + AC_{\bot x} * t_1 \\ AC_y + AC_{\bot y} * t_1 \\ \end{bmatrix}\]Reorder:
\[\begin{bmatrix} -AB_x \\ -AB_y \\ -AC_x \\ -AC_y \\ \end{bmatrix} = \begin{bmatrix} AB_{\bot x} * t_0 - P_x \\ AB_{\bot y} * t_0 - P_y \\ AC_{\bot x} * t_1 - P_x \\ AC_{\bot y} * t_1 - P_y \\ \end{bmatrix}\]Refactor:
\[\begin{bmatrix} -AB_x \\ -AB_y \\ -AC_x \\ -AC_y \\ \end{bmatrix} = \begin{bmatrix} AB_{\bot x} && 0 && -1 && 0 \\ AB_{\bot y} && 0 && 0 && -1 \\ 0 && AC_{\bot x} && -1 && 0 \\ 0 && AC_{\bot y} && 0 && -1 \\ \end{bmatrix} * \begin{bmatrix} t_0 \\ t_1 \\ P_x \\ P_y \\ \end{bmatrix}\]Now we just need to multiply both sides of the equation by the inverse:
\[\begin{bmatrix} AB_{\bot x} && 0 && -1 && 0 \\ AB_{\bot y} && 0 && 0 && -1 \\ 0 && AC_{\bot x} && -1 && 0 \\ 0 && AC_{\bot y} && 0 && -1 \\ \end{bmatrix} ^{-1} * \begin{bmatrix} -AB_x \\ -AB_y \\ -AC_x \\ -AC_y \\ \end{bmatrix} = \begin{bmatrix} t_0 \\ t_1 \\ P_x \\ P_y \\ \end{bmatrix}\]That’s why matrices rule. Now the inverse for such a blocky matrix could be found with wolfram expression:
inverse { {a, 0, -1, 0}, {b, 0, 0, -1}, {0, c, -1, 0}, {0, d, 0, -1} }
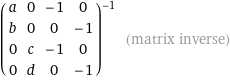 =
= 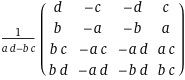
Now we only need to multiply this matrix with a vector and we’re done! I’m too lazy to write all that stuff with latex and probably did some mistakes, so follow this link for complete solution(there are multiple actually):
p_0 = (((a_0 - c_0) * (a_0 + c_0) + (a_1 - c_1) * (a_1 + c_1)) / 2 * (b_1 - c_1)
- ((b_0 - c_0) * (b_0 + c_0) + (b_1 - c_1) * (b_1 + c_1)) / 2 * (a_1 - c_1))
/ D
p_1 = (((b_0 - c_0) * (b_0 + c_0) + (b_1 - c_1) * (b_1 + c_1)) / 2 * (a_0 - c_0)
- ((a_0 - c_0) * (a_0 + c_0) + (a_1 - c_1) * (a_1 + c_1)) / 2 * (b_0 - c_0))
/ D
where D = (a_0 - c_0) * (b_1 - c_1) - (b_0 - c_0) * (a_1 - c_1)
And of course, there’s a much better solution using barycentrics and the Law of Sines.