Adding MLP support to AutoGrad
Table of contents
Post
In the previous post I’ve added support for tensors to the toy automatic differentiation system. Tensors are basically a linear array with a rule to access it in a multi-dimensional fasion.
In this update I’ll extend it to handle MLPs. And for that we need to add a linear layer aka matrix multiplication. First thing we add is a Matrix class, right next to the learnable parameter class. Its job is to own a array of learnable parameters [out_features, in_channels]. The way it works in this setup is that we don’t care about the actual shape of the tensor, all we need to know is that it is an array of N * [in_features], then what we do is we multiply each such array by the matrix and the result is a new array of N * [out_features].
Next thing we need to add the matrix multiplication node, its job is to take a node that produces a tensor and a node that produces the matrix, and multiply the last channels of the tensor by the matrix to produces a new tensor. Next we use that to backpropagate the gradient. If you do the math you’ll see that gradients to the tensor are just gradients of this node multiplied by the transpose matrix, and gradients for the weights is an outer product of the node’s gradients and the input channels. That’s coming up from the basic rules of back propagation for addition and multiplication.
Next I add LeakyReLU activation function for chaining matrix multiplies together to comprise the feedforward MLP pass. Another thing we need is an optimizer. For that I implemented a basic AdamW without variance bias corrections. AdamW is a variant of the Adam optimizer that decouples weight decay from the optimization steps. Meaning that the weight decay is applied directly to the weights after the update step, rather than being included in the loss function and gradients. The function is pretty similar we just keep an exponential running average for grad and grad*grad, basically new_val=lerp(old_val, update, 0.1) - that’s just TAA applied to the grads. Then we divide the mean grad by the square root of the second moment. The second moment is equals to mean^2 + variance. This acts as a dynamic scale for the gradient, the bigger the variance, the smaller the learning rate which helps a lot to stabilize the training. It actually works unreasonably well for a simple technique like this. One thing I’ve omitted is the statistical bias correction but you can look it up.
Source Code:
import math
import random
def make_array(dim):
arr = []
for _ in range(dim):
arr.append(0.0)
return arr
def dims_get_total(dims):
total = 1
for d in dims:
total *= d
return total
"""
New basic building block class for compute.
Basically a flat array with a rule for accessing elements.
We're using a basic rule of linear strides.
"""
class Tensor:
def __init__(self, shape):
self.shape = shape
self.data = make_array(dims_get_total(shape))
self.strides = []
self._compute_strides()
def _compute_strides(self):
total = 1
for d in reversed(self.shape):
self.strides.insert(0, total)
total *= d
def _get_flat_index(self, indices):
if len(indices) != len(self.shape):
raise ValueError("Incorrect number of indices")
index = 0
for i, idx in enumerate(indices):
if not (0 <= idx < self.shape[i]):
raise IndexError("Index out of bounds")
index += idx * self.strides[i]
return index
def __getitem__(self, indices):
index = self._get_flat_index(indices)
return self.data[index]
def __setitem__(self, indices, value):
index = self._get_flat_index(indices)
self.data[index] = value
def __repr__(self):
return f"Tensor(shape={self.shape}, data={self.data})"
def __add__(self, other):
if isinstance(other, (int, float)):
result = Tensor(self.shape)
for i in range(len(self.data)):
result.data[i] = self.data[i] + other
return result
if not isinstance(other, Tensor):
raise TypeError(f"Unsupported operand type: {type(other)}")
if self.shape != other.shape:
raise ValueError(f"Shapes must be the same: {self.shape} vs {other.shape}")
result = Tensor(self.shape)
for i in range(len(self.data)):
result.data[i] = self.data[i] + other.data[i]
return result
def __mul__(self, other):
if isinstance(other, (int, float)):
result = Tensor(self.shape)
for i in range(len(self.data)):
result.data[i] = self.data[i] * other
return result
if not isinstance(other, Tensor):
raise TypeError(f"Unsupported operand type: {type(other)}")
if self.shape != other.shape:
raise ValueError(f"Shapes must be the same: {self.shape} vs {other.shape}")
result = Tensor(self.shape)
for i in range(len(self.data)):
result.data[i] = self.data[i] * other.data[i]
return result
def __sub__(self, other):
if isinstance(other, (int, float)):
result = Tensor(self.shape)
for i in range(len(self.data)):
result.data[i] = self.data[i] - other
return result
if not isinstance(other, Tensor):
raise TypeError(f"Unsupported operand type: {type(other)}")
if self.shape != other.shape:
raise ValueError(f"Shapes must be the same: {self.shape} vs {other.shape}")
result = Tensor(self.shape)
for i in range(len(self.data)):
result.data[i] = self.data[i] - other.data[i]
return result
def __truediv__(self, other):
if isinstance(other, (int, float)):
result = Tensor(self.shape)
for i in range(len(self.data)):
result.data[i] = self.data[i] / other
return result
if not isinstance(other, Tensor):
raise TypeError(f"Unsupported operand type: {type(other)}")
if self.shape != other.shape:
raise ValueError(f"Shapes must be the same: {self.shape} vs {other.shape}")
result = Tensor(self.shape)
for i in range(len(self.data)):
result.data[i] = self.data[i] / other.data[i]
return result
def abs(self):
result = Tensor(self.shape)
for i in range(len(self.data)):
result.data[i] = abs(self.data[i])
return result
def get_list_shape(lst):
shape = []
while isinstance(lst, list):
shape.append(len(lst))
lst = lst[0] if lst else []
return shape
def linearize_list(lst):
result = []
def recurse(sublist):
if isinstance(sublist, list):
for item in sublist:
recurse(item)
else:
result.append(sublist)
recurse(lst)
return result
def tensor_from_list(lst):
shape = get_list_shape(lst)
tensor = Tensor(shape)
tensor.data = linearize_list(lst)
return tensor
# Compute graph basic building block
class AutoGradNode:
def __init__(self, shape):
# scalar valued gradient accumulator for the final dL/dp
self.shape = shape
self.grad = Tensor(shape)
# dependencies for causation sort
self.dependencies = []
def zero_grad(self):
self.grad = Tensor(shape=self.shape)
# Overload operators to build the computation graph
def __add__(self, other): return Add(self, other)
def __mul__(self, other): return Mul(self, other)
def __sub__(self, other): return Sub(self, other)
# Get a topologically sorted list of dependencies
# starts from the leaf nodes and terminates at the root
def get_topo_sorted_list_of_deps(self):
visited = set()
topo_order = []
def dfs(node): # depth-first search
if node in visited:
return
visited.add(node)
for dep in node.dependencies:
dfs(dep)
topo_order.append(node)
dfs(self)
return topo_order
def get_pretty_name(self): return self.__class__.__name__
# Pretty print the computation graph in DOT format
def pretty_print_dot_graph(self):
topo_order = self.get_topo_sorted_list_of_deps()
_str = ""
_str += "digraph G {\n"
for node in topo_order:
_str += f" {id(node)} [label=\"{node.get_pretty_name()}\"];\n"
for dep in node.dependencies:
_str += f" {id(node)} -> {id(dep)};\n"
_str += "}"
return _str
def backward(self):
topo_order = self.get_topo_sorted_list_of_deps()
for node in topo_order:
node.zero_grad() # we don't want to accumulate gradients
for i in range(len(self.grad.data)):
self.grad.data[i] = 1.0 # seed the gradient at the output node dL/dL=1
# Reverse the topological order for backpropagation to start from the output
for node in reversed(topo_order):
# from the tip of the graph down to leaf learnable parameters
# Distribute gradients
node._backward()
# The job of this method is to propagate gradients backward through the network
def _backward(self):
assert False, "Not implemented in base class"
# Materialize the numerical value at the node
# i.e. Evaluate the computation graph
def materialize(self):
assert False, "Not implemented in base class"
# Any value that is not learnable
class Variable(AutoGradNode):
def __init__(self, values, name=None):
assert isinstance(values, Tensor), "Values must be a Tensor"
super().__init__(shape=values.shape)
self.values = values
self.name = name
def get_pretty_name(self):
if self.name:
return f"Variable({self.name})"
else:
return f"Constant({[f'{round(v, 3)}' for v in self.values.data]})"
def materialize(self): return self.values
def _backward(self):
pass
Constant = Variable
# Learnable parameter with initial random value 0..1
class LearnableParameter(AutoGradNode):
def __init__(self, shape):
super().__init__(shape=shape)
self.values = Tensor(shape)
for i in range(len(self.values.data)):
self.values.data[i] = random.random()
def get_pretty_name(self):
if len(self.values.data) <= 3:
return f"LearnableParameter({[round(v, 3) for v in self.values.data]})"
else:
return f"LearnableParameter(shape={self.values.shape})"
def materialize(self): return self.values
def _backward(self):
pass
class Matrix(AutoGradNode):
def __init__(self, in_channels, out_features):
super().__init__(shape=[out_features, in_channels])
self.values = Tensor([out_features, in_channels])
for i in range(len(self.values.data)):
self.values.data[i] = random.random()
def get_pretty_name(self):
return f"Matrix({self.values.shape})"
def materialize(self):
return self.values
def _backward(self):
pass
def transposed(self):
in_features = self.values.shape[1]
out_features = self.values.shape[0]
transposed = Matrix(in_channels=out_features, out_features=in_features)
for i in range(out_features):
for j in range(in_features):
transposed.values.data[i * in_features + j] = self.values.data[j * out_features + i]
return transposed
def tensor_matrix_multiply(tensor, matrix):
in_features = tensor.shape[-1]
out_features = matrix.shape[0]
assert in_features == matrix.shape[1], f"Incompatible matrix dimensions {tensor.shape} and {matrix.shape}"
result = Tensor(tensor.shape[:-1] + [out_features])
total_number_of_elems = len(result.data) # we don't really care about the actual shape, for this we know that the tensor is an array of input features
for s in range(total_number_of_elems // out_features):
for i in range(out_features):
for j in range(in_features):
result.data[s * out_features + i] += tensor.data[s * in_features + j] * matrix.data[i * in_features + j]
return result
def tensor_outer_product(tensor_a, tensor_b):
in_features = tensor_a.shape[-1]
out_features = tensor_b.shape[-1]
result_shape = [out_features, in_features] # tensor_a.shape[:-1] + [out_features, in_features]
result = Tensor(result_shape)
total_number_of_elems_a = len(tensor_a.data) # we don't really care about the actual shape, for this we know that the tensor is an array of input features
total_number_of_elems_b = len(tensor_b.data) # we don't really care about the actual shape, for this we know that the tensor is an array of output features
assert total_number_of_elems_a // in_features == total_number_of_elems_b // out_features, "Incompatible tensor dimensions for outer product"
for s in range(total_number_of_elems_a // in_features):
for i in range(out_features):
for j in range(in_features):
# s * in_features * out_features +
result.data[i * in_features + j] += tensor_a.data[s * in_features + j] * tensor_b.data[s * out_features + i]
return result
class VectorMatrixMultiply(AutoGradNode):
def __init__(self, tensor, matrix):
assert tensor.shape[-1] == matrix.shape[1], "Incompatible matrix dimensions"
super().__init__(shape=tensor.shape[:-1] + [matrix.shape[0]])
self.tensor = tensor
self.matrix = matrix
self.dependencies = [tensor, matrix]
def materialize(self):
tensor = self.tensor.materialize()
matrix = self.matrix.materialize()
return tensor_matrix_multiply(tensor, matrix)
def _backward(self):
# print(f"VectorMatrixMultiply backward")
# print(f"grad : {self.grad}")
# print(f"tensor : {self.tensor.materialize()}")
# print(f"matrix : {self.matrix.materialize()}")
# print(f"mT : {mT.materialize()}")
mT = self.matrix.transposed()
tmp = tensor_matrix_multiply(self.grad, mT.materialize())
self.tensor.grad = self.tensor.grad + tmp
self.matrix.grad = self.matrix.grad + tensor_outer_product(self.tensor.materialize(), self.grad)
class LeakyRelu(AutoGradNode):
def __init__(self, a, negative_slope=0.01):
super().__init__(shape=a.shape)
self.a = a
self.negative_slope = negative_slope
self.dependencies = [a]
def materialize(self):
x = self.a.materialize()
result = Tensor(x.shape)
for i in range(len(x.data)):
result.data[i] = x.data[i] if x.data[i] > 0 else self.negative_slope * x.data[i]
return result
def _backward(self):
am = self.a.materialize()
slope = Tensor(self.a.shape)
for i in range(len(am.data)):
slope.data[i] = 1.0 if am.data[i] > 0.0 else self.negative_slope
self.a.grad = self.a.grad + self.grad * slope
class Reduce(AutoGradNode):
def __init__(self, a, op='+'):
super().__init__(shape=[1,])
self.a = a
self.dependencies = [a]
self.op = op
assert op in ['+'], "Only sum reduction is supported"
def materialize(self): return tensor_from_list([sum(self.a.materialize().data)])
def _backward(self):
self.a.grad = self.a.grad + self.grad.data[0] # broadcast the gradient
class Square(AutoGradNode):
def __init__(self, a):
super().__init__(shape=a.shape)
self.a = a
self.dependencies = [a]
def materialize(self):
x = self.a.materialize()
return x * x
def _backward(self):
self.a.grad = self.a.grad + self.grad * 2.0 * self.a.materialize()
class Sub(AutoGradNode):
def __init__(self, a, b):
assert a.shape == b.shape, "Incompatible tensor dimensions"
super().__init__(shape=a.shape)
self.a = a
self.b = b
self.dependencies = [a, b]
def materialize(self):
return self.a.materialize() - self.b.materialize()
def _backward(self):
self.a.grad = self.a.grad + self.grad
self.b.grad = self.b.grad - self.grad
class Add(AutoGradNode):
def __init__(self, a, b):
assert a.shape == b.shape, "Incompatible tensor dimensions"
super().__init__(shape=a.shape)
self.a = a
self.b = b
self.dependencies = [a, b]
def materialize(self):
return self.a.materialize() + self.b.materialize()
def _backward(self):
self.a.grad = self.a.grad + self.grad
self.b.grad = self.b.grad + self.grad
class Mul(AutoGradNode):
def __init__(self, a, b):
assert a.shape == b.shape, "Incompatible tensor dimensions"
super().__init__(shape=a.shape)
self.a = a
self.b = b
self.dependencies = [a, b]
def materialize(self):
return self.a.materialize() * self.b.materialize()
def _backward(self):
self.a.grad = self.a.grad + self.grad * self.b.materialize()
self.b.grad = self.b.grad + self.grad * self.a.materialize()
class Sin(AutoGradNode):
def __init__(self, a):
super().__init__(shape=a.shape)
self.a = a
self.dependencies = [a]
def materialize(self):
ma = self.a.materialize()
result = Tensor(ma.shape)
for i in range(len(ma.data)):
result.data[i] = math.sin(ma.data[i])
return result
def _backward(self):
ma = self.a.materialize()
for i in range(len(ma.data)):
self.a.grad.data[i] = self.a.grad.data[i] + self.grad.data[i] * math.cos(ma.data[i])
num_nodes = 64
m0 = Matrix(in_channels=1, out_features=num_nodes)
b0 = LearnableParameter(shape=[num_nodes,]) # bias
m1 = Matrix(in_channels=num_nodes, out_features=num_nodes)
b1 = LearnableParameter(shape=[num_nodes,]) # bias
m2 = Matrix(in_channels=num_nodes, out_features=1)
b2 = LearnableParameter(shape=[1,]) # bias
def eval_mlp(x):
z = VectorMatrixMultiply(tensor=x, matrix=m0)
z = z + b0
z = LeakyRelu(z, negative_slope=0.1)
z = VectorMatrixMultiply(tensor=z, matrix=m1)
z = z + b1
z = LeakyRelu(z, negative_slope=0.1)
z = VectorMatrixMultiply(tensor=z, matrix=m2)
z = z + b2
return z
def eval_target(x):
return Square(x) * Constant(tensor_from_list([2.777, ])) + Constant(tensor_from_list([0.123,])) - x * x * x * Constant(tensor_from_list([1.5,])) + Sin(x * Constant(tensor_from_list([4.0,])))
class AdamW:
"""
Simple AdamW without variance bias correction
"""
def __init__(self, parameters, lr=0.001, betas=(0.9, 0.999), weight_decay=0.01):
self.parameters = parameters
self.lr = lr
self.betas = betas
self.weight_decay = weight_decay
self.moments_1 = []
self.moments_2 = []
for p in parameters:
self.moments_1.append(Tensor(p.grad.shape))
self.moments_2.append(Tensor(p.grad.shape))
def step(self):
for i, p in enumerate(self.parameters):
self.moments_1[i] = self.moments_1[i] * self.betas[0] + p.grad * (1 - self.betas[0])
self.moments_2[i] = self.moments_2[i] * self.betas[1] + (p.grad * p.grad) * (1 - self.betas[1])
variance = self.moments_2[i] - self.moments_1[i] * self.moments_1[i]
for didx in range(len(p.values.data)):
p.values.data[didx] -= self.lr * self.moments_1[i].data[didx] / (math.sqrt(self.moments_2[i].data[didx]) + 1e-8)
p.values.data[didx] -= self.weight_decay * self.lr * p.values.data[didx]
adamw = AdamW(parameters=[m0, b0, m1, b1, m2, b2], lr=0.001, weight_decay=0.001, betas=(0.9, 0.9))
for epoch in range(3000):
x = Variable(tensor_from_list([random.random() * 2.0 - 1.0,]), name="x")
mlp = eval_mlp(x)
loss = Reduce(Square(mlp - eval_target(x))) # L2 loss to Ax^2+B
print(f"Epoch {epoch}: loss = {loss.materialize()};")
# Backward pass
# Gradient reset happens internally in the backward pass
loss.backward()
adamw.step()
with open(".tmp/graph.dot", "w") as f:
f.write(loss.pretty_print_dot_graph())
# Plot our mlp
import matplotlib.pyplot as plt
max_range = 100
x_test_vals = [(i / max_range - 1.0) for i in range(2 * max_range)]
y_test_vals = []
for x in x_test_vals:
y_test_vals.append(eval_mlp(Variable(tensor_from_list([x,]), name="x")).materialize().data[0])
x_ref_vals = [(i / max_range - 1.0) for i in range(2 * max_range)]
y_ref_vals = []
for x in x_ref_vals:
y_ref_vals.append(eval_target(Variable(tensor_from_list([x,]), name="x")).materialize().data[0])
plt.plot(x_test_vals, y_test_vals, label="MLP")
plt.plot(x_ref_vals, y_ref_vals, label="Target", linestyle="--")
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
After a few minutes you should get this plot:
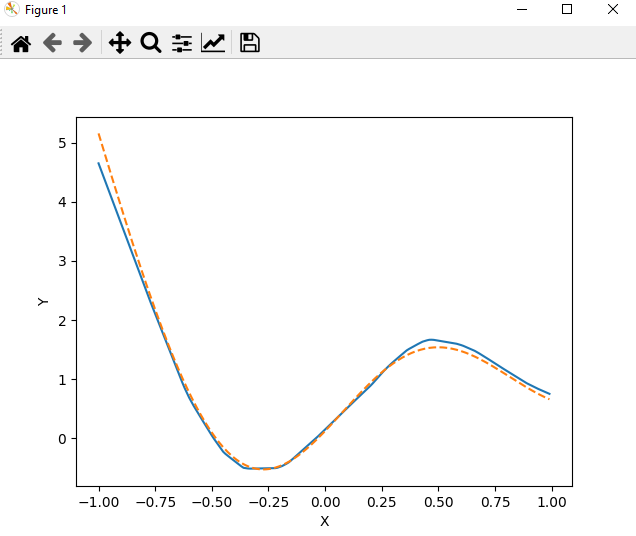
The dotted line represents the target function we are trying to learn, while the solid line represents the output of our MLP. As you can see, the MLP is able to learn the target function quite well.
This is our compute graph:
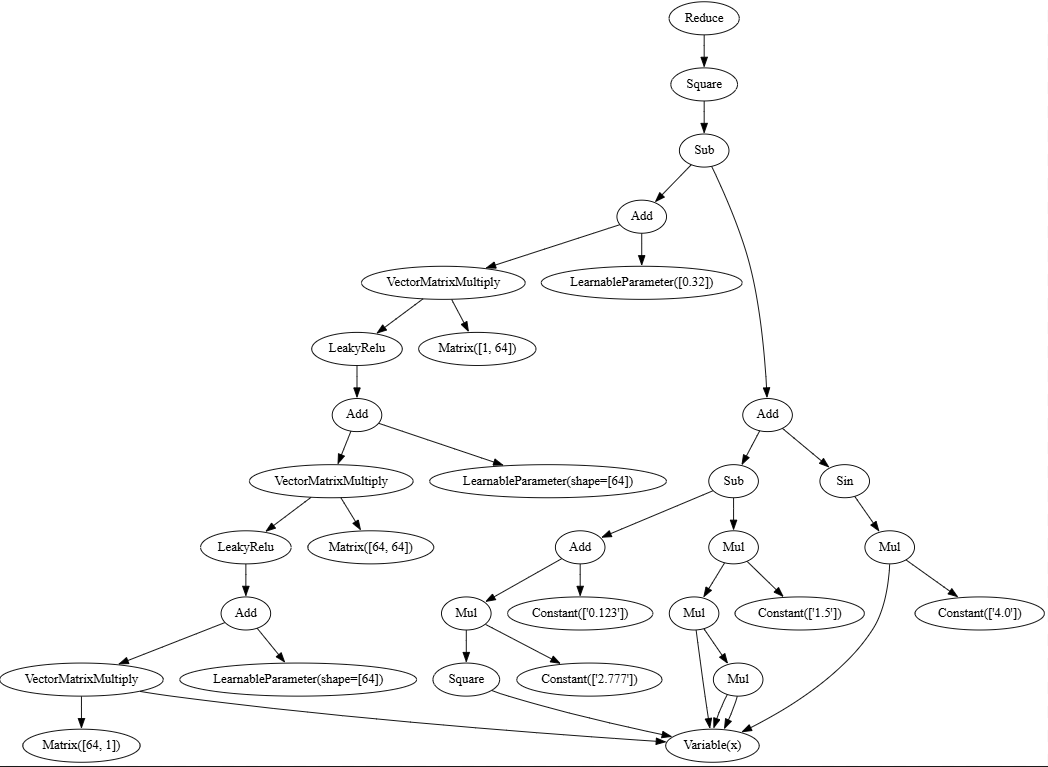
It looks like we have 2 branches in the computation graph: 1 for the MLP and the other for the target function. In reality we can replace the target function by just raw data and it will yield the same result. So you could think of MLP as being an automatic approximation discovery mechanism to a black box.