Generating Cats with KPN Filtering
Table of contents
About
This is a short post to collect some references and notes about generative modeling and to try to experiment with generating images of cats using KPN denoising in pixel space. It’s not a comprehensive technical report, rather I was just curious if I get anything at all with this approach.
Post
Usually for image generation diffusion models operate in latent space [3] using direct prediction of noise, but I wanted to see how well it works in pixel space by using KPN bilateral filters and on top of that predict the low rank target directly, instead of predicting noised velocity, this allows to have a low rank bottleneck that can help with generalization and reduce the capacity of the network compared to those that need to be predicting full rank off-manifold targets.
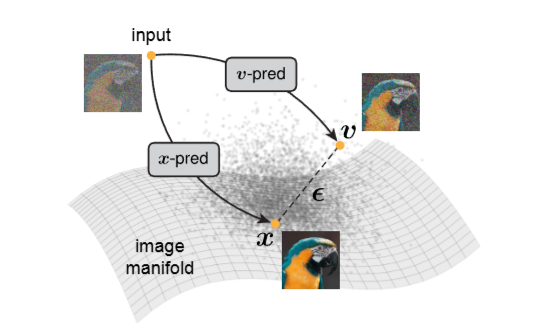
src [4]
So what I’m trying is iterative projection to the low rank manifold using a denoising kernel operator.
The advantage of KPN is that it has a really good regularization bias as well as behaving well after quantization which makes it suitable for deployment on edge devices. Also KPN filters can be efficiently implemented on GPUs.
The model is trained on 64x64 images of cats from the Cats faces 64x64 (For generative models) using an architecture with a 8x8 patch transformer in the backbone and a stack of upscaling convolutions that drive KPN filtering network for denoising. The training process involves lerping the image to Gaussian noise, such that information is gradually lost and then training the model to predict the original image from that noised input using L2 and LPIPS [7].
The problem with bilateral filters is that they compute the output as a convex combination of input pixels, which makes it hard to create information that is not already present in the input. To mitigate this, I use a separate low capacity network to predict color drift(bias) that is added after the filtering step, the architecure of the drift prediction model is much simpler which guarantees that it doesn’t do the heavy lifting. Also, I do not normalize the bilateral weights to sum to 1 and allow them to be negative with tanh(x) activation. This makes the filtering non-convex and helps to introduce new colors and details that were destroyed by the noising process.
For filtering network I use a simplified version of partitioning pyramids from Neural Partitioning Pyramids for Denoising Monte Carlo Renderings :
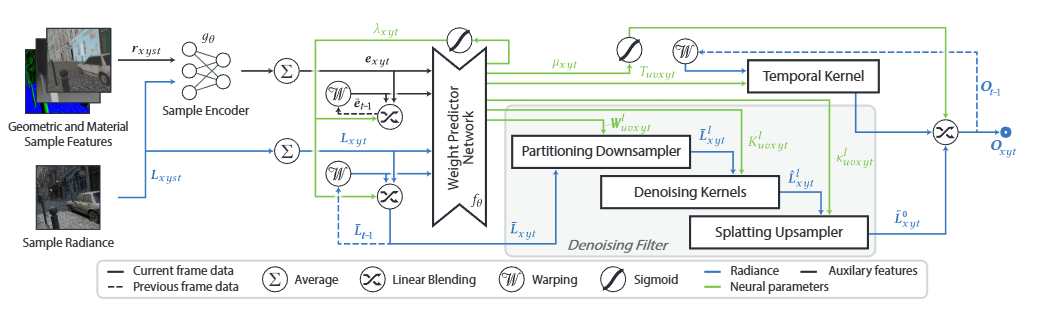
With a few tricks from Bartlomiej Wronski: Procedural Kernel Networks to make it more efficient:

Like using the low rank precision matrix gaussian parametrization to reduce the number of parameters needed for the kernel prediction.
For filtering network I use 5x5 spatial kernels followed for downsampling by 2x2 average pooling, and for upsampling I use low rank gaussian 5x5 with sigmoid lerp with the skip, so it’s like a unet but for the image.
For color drift prediction I use a small U-Net that operates on RGB 64x64 source images and predicts per pixel channel offsets that are added after the filtering step.
The idea is that potentially the low detail color drift can be predicted more easily than the full image, as it only needs to capture the low frequency components of the image. And it would run in full precision which helps with color fidelity while the KPN filtering can be quantized more aggressively.
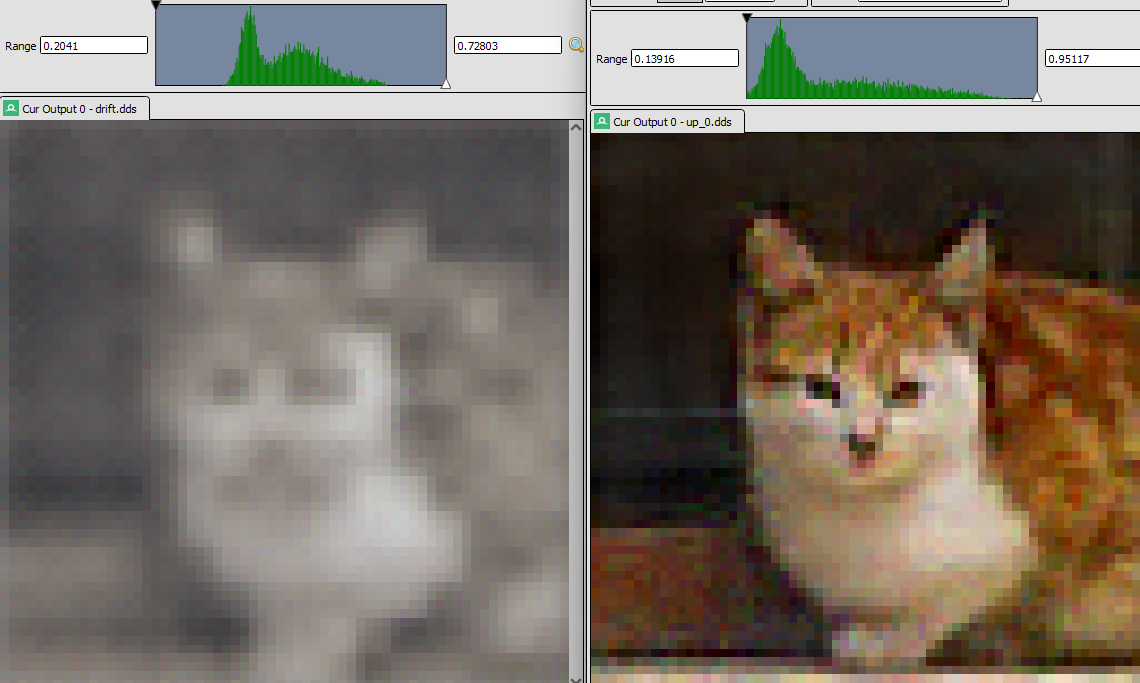
Drift on the left, KPN filtered output on the right.
Results
Here are some generated samples after training for about 5k epochs. Nothing impressive, but interesting as a ‘proof of concept’.


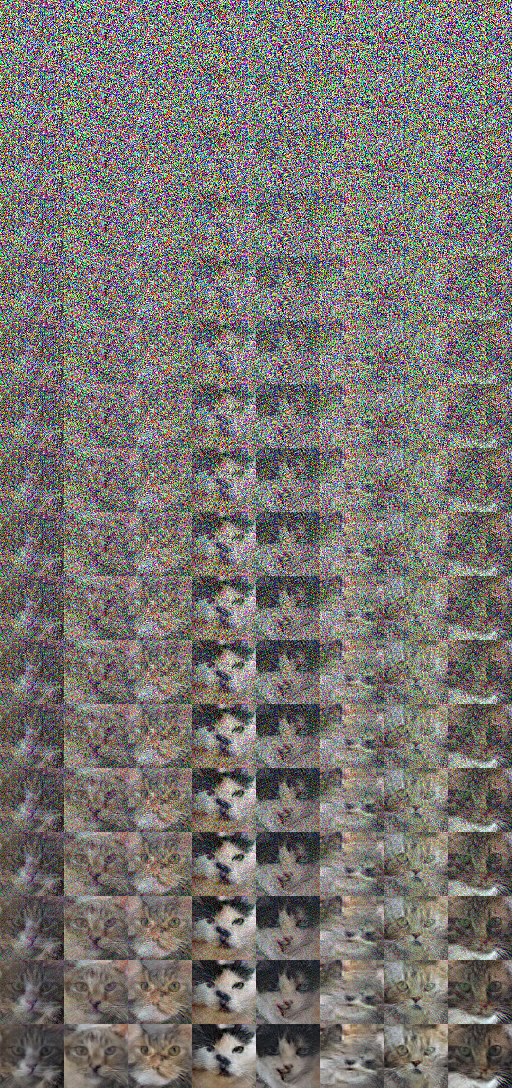
Links
[1]Understand Diffusion Models with VAEs
[2]Variational Autoencoders and Diffusion Models
[3]Generative modelling in latent space
[4]Back to Basics: Let Denoising Generative Models Denoise
[5]Neural Partitioning Pyramids for Denoising Monte Carlo Renderings
[6]Bartlomiej Wronski: Procedural Kernel Networks
[7]The Unreasonable Effectiveness of Deep Features as a Perceptual Metric