Adding vector support to AutoGrad
Table of contents
Post
In the previous post I’ve demonstrated how to build a toy automatic differentiation system from the first principles. It only handled the scalar parameters thought. In this update I’ll extend it to handle vectors. The change is quite trivial, actually, all we need to do is to handle arrays of values and after that everything is the same. The only other change is adding a Reduce operator to finally map our vector outputs to the scalar loss.
import math
import random
def make_array(dim):
arr = []
for _ in range(dim):
arr.append(0.0)
return arr
# Compute graph basic building block
class AutoGradNode:
def __init__(self, dim=1):
# scalar valued gradient accumulator for the final dL/dp
self.dim = dim
self.grad = make_array(dim)
# dependencies for causation sort
self.dependencies = []
def zero_grad(self):
for i in range(len(self.grad)):
self.grad[i] = 0.0
# Overload operators to build the computation graph
def __add__(self, other): return Add(self, other)
def __mul__(self, other): return Mul(self, other)
def __sub__(self, other): return Sub(self, other)
# Get a topologically sorted list of dependencies
# starts from the leaf nodes and terminates at the root
def get_topo_sorted_list_of_deps(self):
visited = set()
topo_order = []
def dfs(node): # depth-first search
if node in visited:
return
visited.add(node)
for dep in node.dependencies:
dfs(dep)
topo_order.append(node)
dfs(self)
return topo_order
def get_pretty_name(self): return self.__class__.__name__
# Pretty print the computation graph in DOT format
def pretty_print_dot_graph(self):
topo_order = self.get_topo_sorted_list_of_deps()
_str = ""
_str += "digraph G {\n"
for node in topo_order:
_str += f" {id(node)} [label=\"{node.get_pretty_name()}\"];\n"
for dep in node.dependencies:
_str += f" {id(node)} -> {id(dep)};\n"
_str += "}"
return _str
def backward(self):
topo_order = self.get_topo_sorted_list_of_deps()
for node in topo_order:
node.zero_grad() # we don't want to accumulate gradients
for i in range(len(self.grad)):
self.grad[i] = 1.0 # seed the gradient at the output node
# Reverse the topological order for backpropagation to start from the output
for node in reversed(topo_order):
# from the tip of the graph down to leaf learnable parameters
# Distribute gradients
node._backward()
# The job of this method is to propagate gradients backward through the network
def _backward(self):
assert False, "Not implemented in base class"
# Materialize the numerical value at the node
# i.e. Evaluate the computation graph
def materialize(self):
assert False, "Not implemented in base class"
# Any value that is not learnable
class Variable(AutoGradNode):
def __init__(self, values, name=None):
assert isinstance(values, list), "Values must be a list"
super().__init__(dim=len(values))
self.values = values
self.name = name
def get_pretty_name(self):
if self.name:
return f"Variable({self.name})"
else:
return f"Constant({[f'{round(v, 3)}' for v in self.values]})"
def materialize(self): return self.values
def _backward(self):
pass
Constant = Variable
# Learnable parameter with initial random value 0..1
class LearnableParameter(AutoGradNode):
def __init__(self, dim):
super().__init__(dim=dim)
self.values = make_array(dim)
for i in range(dim):
self.values[i] = random.random()
def get_pretty_name(self):
return f"LearnableParameter({[round(v, 3) for v in self.values]})"
def materialize(self): return self.values
def _backward(self):
pass
# Reduce the tensor to along a dimension by applying a binary operator to all of its elements
class Reduce(AutoGradNode):
def __init__(self, a, op='+'):
super().__init__(dim=1)
self.a = a
self.dependencies = [a]
self.op = op
assert op in ['+'], "Only sum reduction is supported"
def materialize(self): return [sum(self.a.materialize())]
def _backward(self):
for i in range(len(self.a.grad)):
self.a.grad[i] += self.grad[0] # broadcast the gradient
class Abs(AutoGradNode):
def __init__(self, a):
super().__init__(dim=a.dim)
self.a = a
self.dependencies = [a]
def materialize(self):
return [abs(x) for x in self.a.materialize()]
def _backward(self):
materialized = self.a.materialize()
for i in range(len(self.a.grad)):
self.a.grad[i] += self.grad[i] * (1.0 if materialized[i] > 0 else -1.0)
class Square(AutoGradNode):
def __init__(self, a):
super().__init__(dim=a.dim)
self.a = a
self.dependencies = [a]
def materialize(self):
return [x ** 2 for x in self.a.materialize()]
def _backward(self):
materialized = self.a.materialize()
for i in range(len(self.a.grad)):
self.a.grad[i] += self.grad[i] * 2.0 * materialized[i]
class Sqrt(AutoGradNode):
def __init__(self, a):
super().__init__(dim=a.dim)
self.a = a
self.dependencies = [a]
def materialize(self):
return [x ** 0.5 for x in self.a.materialize()]
def _backward(self):
materialized = self.a.materialize()
for i in range(len(self.a.grad)):
self.a.grad[i] += self.grad[i] * 0.5 * (materialized[i] ** -0.5)
class Sub(AutoGradNode):
def __init__(self, a, b):
assert a.dim == b.dim, "Incompatible tensor dimensions"
super().__init__(dim=a.dim)
self.a = a
self.b = b
self.dependencies = [a, b]
def materialize(self):
return [a - b for a, b in zip(self.a.materialize(), self.b.materialize())]
def _backward(self):
for i in range(len(self.a.grad)):
self.a.grad[i] += self.grad[i]
for i in range(len(self.b.grad)):
self.b.grad[i] -= self.grad[i]
class Add(AutoGradNode):
def __init__(self, a, b):
assert a.dim == b.dim, "Incompatible tensor dimensions"
super().__init__(dim=a.dim)
self.a = a
self.b = b
self.dependencies = [a, b]
def materialize(self):
return [a + b for a, b in zip(self.a.materialize(), self.b.materialize())]
def _backward(self):
for i in range(len(self.a.grad)):
self.a.grad[i] += self.grad[i]
for i in range(len(self.b.grad)):
self.b.grad[i] += self.grad[i]
class Mul(AutoGradNode):
def __init__(self, a, b):
assert a.dim == b.dim, "Incompatible tensor dimensions"
super().__init__(dim=a.dim)
self.a = a
self.b = b
self.dependencies = [a, b]
def materialize(self):
return [a * b for a, b in zip(self.a.materialize(), self.b.materialize())]
def _backward(self):
materialized_a = self.a.materialize()
materialized_b = self.b.materialize()
for i in range(len(self.a.grad)):
self.a.grad[i] += self.grad[i] * materialized_b[i]
for i in range(len(self.b.grad)):
self.b.grad[i] += self.grad[i] * materialized_a[i]
a = LearnableParameter(dim=3)
b = LearnableParameter(dim=3)
for epoch in range(3000):
x = Variable([random.random(), random.random(), random.random()], name="x")
z = Square(x) * a + b
loss = Reduce(Square(z - (Square(x) * Constant([1.777, 1.333, 0.333]) + Constant([1.55, 0.0, -1.666])))) # L2 loss to Ax^2+B
print(f"Epoch {epoch}: loss = {loss.materialize()}; a = {a.materialize()}, b = {b.materialize()}")
# Backward pass
# Gradient reset happens internally in the backward pass
loss.backward()
# Update parameters
learning_rate = 0.01333
for node in [a, b]:
# print(f"grad = {node.grad}")
for i in range(node.dim):
node.values[i] -= learning_rate * node.grad[i]
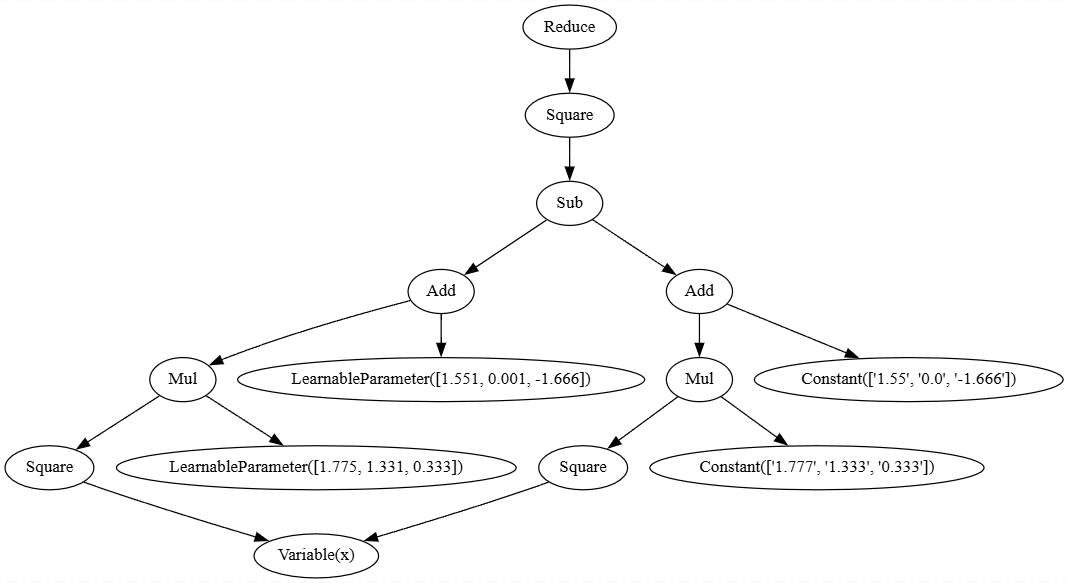
with open(".tmp/graph.dot", "w") as f:
f.write(loss.pretty_print_dot_graph())
# Output:
# Epoch 2999: loss = [1.5098890777062413e-07]; a = [1.775353643899192, 1.3317554153747089, 0.33246132295415703], b = [1.5505584457975028, 0.0004274128487799639, -1.6657681143518706]
# Target: [1.777, 1.333, 0.333], [1.55, 0.0, -1.666]
We get this dotgraph at .tmp/graph.dot: