Image encoding using AutoGrad
Table of contents
Post
In the previous post I’ve added MLP support to the toy AutoGrad framework. In this post I will implement image compression using the AutoGrad framework. We need to start from some low hanging fruit optimizations first. I’ve changed the python array to numpy arrays and fixed up all the uses. The main thing is leveraging einsum to replace manual matrix multiplies and outer products.
# matrix multiply
np_result = np.einsum('si,oi->so', np_tensor, np_matrix)
# outer product + accumulate
np_result = np.einsum('si,sj->ji', np_tensor_a, np_tensor_b)
Basically we reshape everything into [N, C] where C is the number of channels (e.g. RGB). After that all the operations are quite simple, we just use einsum to express them. All we do is treat any tensor as an array of feature vectors for a given operation and then reshape it back to its final shape for the next operation.
This will enable us to have more heavy weight training. In particular, we can now use larger batch sizes and more complex models without waiting for ages.
Our approach for image encoding here is to have an MLP that converts a feature vector with frequency encoding into color value. After that we assemble a group of pixels for a batch and initialize the feature vectors for them and finally pass them through the MLP for training. Then for inference we assemble all the pixels into a large batch i.e. [height, width, channels] -> [height * width, channels] and then after MLP we reshape back to [height, width, RGB].
At the end after a few minutes we can see the encoding results.

Not too bad for 4 layers. You can take a look at the live WebGPU version of the same approach that I’ve implemented here.
Original:

As a bonus we can resample the image to a grid of an arbitrary resolution because of how we structured the MLP.
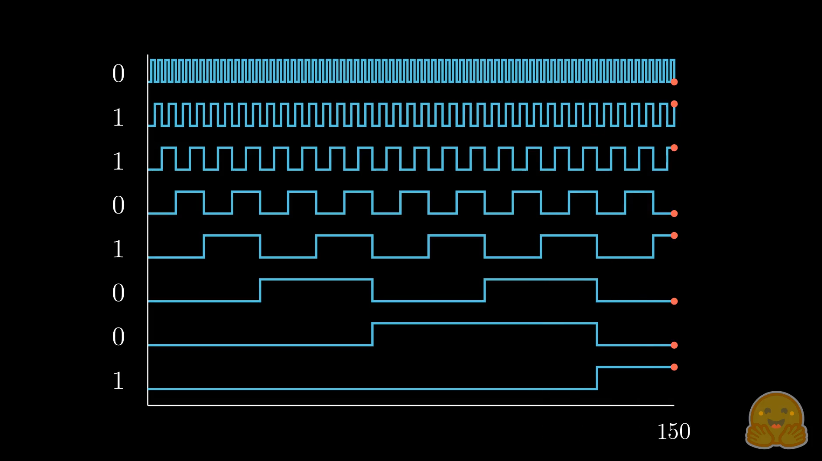
Frequency encoding is a way to encode absolute pixel positions, you could think of it as smooth bits, if you have an integer series 1, 2, 3, … N-1 in the binary form it will be [0b0000, 0b0001, 0b0010, …, 0b1111] for N=16. You can notice that the frequency of each bit is halfed, for neural networks we’d like to add smoothness so that it can generalize. For that we use sin+cos of doubling frequency for each band.
Source Code:
import math
import random
from matplotlib import image
import numpy as np
import ctypes
def make_array(dim):
return np.zeros(dim)
def dims_get_total(dims):
total = 1
for d in dims:
total *= d
return total
"""
New basic building block class for compute.
Basically a flat array with a rule for accessing elements.
We're using a basic rule of linear strides.
"""
class Tensor:
def __init__(self, shape, data=None):
self.shape = shape
if data is not None:
if not isinstance(data, np.ndarray):
data = np.array(data, dtype=np.float32)
self.data = data.flatten()[:]
else:
self.data = make_array(dims_get_total(shape))
self.strides = []
self._compute_strides()
def _compute_strides(self):
total = 1
for d in reversed(self.shape):
self.strides.insert(0, total)
total *= d
def _get_flat_index(self, indices):
if len(indices) != len(self.shape):
raise ValueError("Incorrect number of indices")
index = 0
for i, idx in enumerate(indices):
if not (0 <= idx < self.shape[i]):
raise IndexError("Index out of bounds")
index += idx * self.strides[i]
return index
def __getitem__(self, indices):
index = self._get_flat_index(indices)
return self.data[index]
def __setitem__(self, indices, value):
index = self._get_flat_index(indices)
self.data[index] = value
def __repr__(self):
return f"Tensor(shape={self.shape}, data={self.data})"
def __add__(self, other):
result = Tensor(self.shape)
if isinstance(other, (int, float)):
result.data = self.data + other
else:
result.data = self.data + other.data
return result
def __mul__(self, other):
result = Tensor(self.shape)
if isinstance(other, (int, float)):
result.data = self.data * other
else:
result.data = self.data * other.data
return result
def __sub__(self, other):
result = Tensor(self.shape)
if isinstance(other, (int, float)):
result.data = self.data - other
else:
result.data = self.data - other.data
return result
def __truediv__(self, other):
result = Tensor(self.shape)
if isinstance(other, (int, float)):
result.data = self.data / other
else:
result.data = self.data / other.data
return result
def abs(self):
result = Tensor(self.shape)
result.data = np.abs(self.data)
return result
def get_list_shape(lst):
shape = []
while isinstance(lst, list):
shape.append(len(lst))
lst = lst[0] if lst else []
return shape
def linearize_list(lst):
result = []
def recurse(sublist):
if isinstance(sublist, list):
for item in sublist:
recurse(item)
else:
result.append(sublist)
recurse(lst)
return np.array(result)
def tensor_from_list(lst, shape=None):
if shape is None:
shape = get_list_shape(lst)
tensor = Tensor(shape)
tensor.data = linearize_list(lst)
return tensor
# Compute graph basic building block
class AutoGradNode:
def __init__(self, shape):
# scalar valued gradient accumulator for the final dL/dp
self.shape = shape
self.grad = Tensor(shape)
# dependencies for causation sort
self.dependencies = []
self.materialized = None
def zero_grad(self):
self.grad = Tensor(shape=self.shape)
# Overload operators to build the computation graph
def __add__(self, other): return Add(self, other)
def __mul__(self, other): return Mul(self, other)
def __sub__(self, other): return Sub(self, other)
# Get a topologically sorted list of dependencies
# starts from the leaf nodes and terminates at the root
def get_topo_sorted_list_of_deps(self):
visited = set()
topo_order = []
def dfs(node): # depth-first search
if node in visited:
return
visited.add(node)
for dep in node.dependencies:
dfs(dep)
topo_order.append(node)
dfs(self)
return topo_order
def get_pretty_name(self): return self.__class__.__name__
# Pretty print the computation graph in DOT format
def pretty_print_dot_graph(self):
topo_order = self.get_topo_sorted_list_of_deps()
_str = ""
_str += "digraph G {\n"
for node in topo_order:
_str += f" {id(node)} [label=\"{node.get_pretty_name()}\"];\n"
for dep in node.dependencies:
_str += f" {id(node)} -> {id(dep)};\n"
_str += "}"
return _str
def backward(self):
topo_order = self.get_topo_sorted_list_of_deps()
for node in topo_order:
node.zero_grad() # we don't want to accumulate gradients
for i in range(len(self.grad.data)):
self.grad.data[i] = 1.0 # seed the gradient at the output node dL/dL=1
# Reverse the topological order for backpropagation to start from the output
for node in reversed(topo_order):
# from the tip of the graph down to leaf learnable parameters
# Distribute gradients
node._backward()
# The job of this method is to propagate gradients backward through the network
def _backward(self):
assert False, "Not implemented in base class"
# Materialize the numerical value at the node
# i.e. Evaluate the computation graph
def _materialize(self):
assert False, "Not implemented in base class"
# Cache
def materialize(self):
if self.materialized is None:
self.materialized = self._materialize()
# print(f"Materialized {self.get_pretty_name()}: {self.materialized.shape}")
return self.materialized
# Any value that is not learnable
class Variable(AutoGradNode):
def __init__(self, values, name=None):
assert isinstance(values, Tensor), f"Values must be a Tensor, got {type(values)}"
super().__init__(shape=values.shape)
self.values = values
self.name = name
def get_pretty_name(self):
if self.name:
return f"Variable({self.name})"
else:
return f"Constant({[f'{round(v, 3)}' for v in self.values.data]})"
def _materialize(self): return self.values
def _backward(self):
pass
Constant = Variable
# Learnable parameter with initial random value 0..1
class LearnableParameter(AutoGradNode):
def __init__(self, shape):
super().__init__(shape=shape)
self.values = Tensor(shape)
for i in range(len(self.values.data)):
self.values.data[i] = random.gauss(0.0, 1.0) * (1.0 / math.sqrt(shape[-1]))
def get_pretty_name(self):
if len(self.values.data) <= 3:
return f"LearnableParameter({[round(v, 3) for v in self.values.data]})"
else:
return f"LearnableParameter(shape={self.values.shape})"
def _materialize(self): return self.values
def _backward(self):
pass
class Matrix(AutoGradNode):
def __init__(self, in_channels, out_features):
super().__init__(shape=[out_features, in_channels])
self.values = Tensor([out_features, in_channels])
for i in range(len(self.values.data)):
self.values.data[i] = random.gauss(0.0, 1.0) * (1.0 / math.sqrt(in_channels))
def get_pretty_name(self):
return f"Matrix({self.values.shape})"
def _materialize(self):
return self.values
def _backward(self):
pass
def transposed(self):
in_features = self.values.shape[1]
out_features = self.values.shape[0]
transposed = Matrix(in_channels=out_features, out_features=in_features)
for i in range(out_features):
for j in range(in_features):
transposed.values.data[i * in_features + j] = self.values.data[j * out_features + i]
return transposed
def tensor_matrix_multiply(tensor, matrix):
in_features = tensor.shape[-1]
out_features = matrix.shape[0]
assert in_features == matrix.shape[1], f"Incompatible matrix dimensions {tensor.shape} and {matrix.shape}"
total_number_of_elems = len(tensor.data) # we don't really care about the actual shape, for this we know that the tensor is an array of input features
np_tensor = tensor.data.reshape(total_number_of_elems // in_features, in_features)
np_matrix = matrix.data.reshape(out_features, in_features)
np_result = np.einsum('si,oi->so', np_tensor, np_matrix)
return Tensor(shape=tensor.shape[:-1] + [out_features], data=np_result)
def tensor_outer_product(tensor_a, tensor_b):
in_features = tensor_a.shape[-1]
out_features = tensor_b.shape[-1]
result_shape = [out_features, in_features] # tensor_a.shape[:-1] + [out_features, in_features]
total_number_of_elems_a = len(tensor_a.data) # we don't really care about the actual shape, for this we know that the tensor is an array of input features
total_number_of_elems_b = len(tensor_b.data) # we don't really care about the actual shape, for this we know that the tensor is an array of output features
assert total_number_of_elems_a // in_features == total_number_of_elems_b // out_features, "Incompatible tensor dimensions for outer product"
np_tensor_a = tensor_a.data.reshape(total_number_of_elems_a // in_features, in_features)
np_tensor_b = tensor_b.data.reshape(total_number_of_elems_b // out_features, out_features)
np_result = np.einsum('si,sj->ji', np_tensor_a, np_tensor_b)
return Tensor(shape=result_shape, data=np_result)
class VectorMatrixMultiply(AutoGradNode):
def __init__(self, tensor, matrix):
assert tensor.shape[-1] == matrix.shape[1], f"Incompatible matrix dimensions: {tensor.shape} vs {matrix.shape}"
super().__init__(shape=tensor.shape[:-1] + [matrix.shape[0]])
self.tensor = tensor
self.matrix = matrix
self.dependencies = [tensor, matrix]
def _materialize(self):
tensor = self.tensor.materialize()
matrix = self.matrix.materialize()
return tensor_matrix_multiply(tensor, matrix)
def _backward(self):
self.tensor.grad = self.tensor.grad + tensor_matrix_multiply(self.grad, self.matrix.transposed().materialize())
self.matrix.grad = self.matrix.grad + tensor_outer_product(self.tensor.materialize(), self.grad)
class LeakyRelu(AutoGradNode):
def __init__(self, a, negative_slope=0.01):
super().__init__(shape=a.shape)
self.a = a
self.negative_slope = negative_slope
self.dependencies = [a]
def _materialize(self):
x = self.a.materialize()
result = Tensor(x.shape)
result.data = np.maximum(x.data, self.negative_slope * x.data)
return result
def _backward(self):
am = self.a.materialize()
slope = Tensor(self.a.shape)
slope.data = np.where(am.data > 0.0, 1.0, self.negative_slope)
self.a.grad = self.a.grad + self.grad * slope
class Reduce(AutoGradNode):
def __init__(self, a, op='+'):
super().__init__(shape=[1,])
self.a = a
self.dependencies = [a]
self.op = op
assert op in ['+'], "Only sum reduction is supported"
def _materialize(self): return tensor_from_list([sum(self.a.materialize().data)])
def _backward(self):
self.a.grad = self.a.grad + self.grad.data[0] # broadcast the gradient
class Square(AutoGradNode):
def __init__(self, a):
super().__init__(shape=a.shape)
self.a = a
self.dependencies = [a]
def _materialize(self):
x = self.a.materialize()
return x * x
def _backward(self):
self.a.grad = self.a.grad + self.grad * 2.0 * self.a.materialize()
class Abs(AutoGradNode):
def __init__(self, a):
super().__init__(shape=a.shape)
self.a = a
self.dependencies = [a]
def _materialize(self):
x = self.a.materialize()
result = Tensor(x.shape)
result.data = np.abs(x.data)
return result
def _backward(self):
self.a.grad = self.a.grad + self.grad * np.sign(self.a.materialize().data)
class Exp(AutoGradNode):
def __init__(self, a):
super().__init__(shape=a.shape)
self.a = a
self.dependencies = [a]
def _materialize(self):
x = self.a.materialize()
result = Tensor(x.shape)
result.data = np.exp(x.data)
return result
def _backward(self):
x = self.a.materialize()
self.a.grad = self.a.grad + self.grad * np.exp(x.data)
class Sub(AutoGradNode):
def __init__(self, a, b):
assert a.shape == b.shape, f"Incompatible tensor dimensions: {a.shape} vs {b.shape}"
super().__init__(shape=a.shape)
self.a = a
self.b = b
self.dependencies = [a, b]
def _materialize(self):
return self.a.materialize() - self.b.materialize()
def _backward(self):
self.a.grad = self.a.grad + self.grad
self.b.grad = self.b.grad - self.grad
class Add(AutoGradNode):
def __init__(self, a, b):
assert a.shape == b.shape, f"Incompatible tensor dimensions: {a.shape} vs {b.shape}"
super().__init__(shape=a.shape)
self.a = a
self.b = b
self.dependencies = [a, b]
def _materialize(self):
return self.a.materialize() + self.b.materialize()
def _backward(self):
self.a.grad = self.a.grad + self.grad
self.b.grad = self.b.grad + self.grad
class Mul(AutoGradNode):
def __init__(self, a, b):
assert a.shape == b.shape, f"Incompatible tensor dimensions: {a.shape} vs {b.shape}"
super().__init__(shape=a.shape)
self.a = a
self.b = b
self.dependencies = [a, b]
def _materialize(self):
return self.a.materialize() * self.b.materialize()
def _backward(self):
self.a.grad = self.a.grad + self.grad * self.b.materialize()
self.b.grad = self.b.grad + self.grad * self.a.materialize()
class Sin(AutoGradNode):
def __init__(self, a):
super().__init__(shape=a.shape)
self.a = a
self.dependencies = [a]
def _materialize(self):
ma = self.a.materialize()
result = Tensor(ma.shape)
result.data = np.sin(ma.data)
return result
def _backward(self):
ma = self.a.materialize()
self.a.grad.data = self.a.grad.data + self.grad.data * np.cos(ma.data)
class Broadcast(AutoGradNode):
def __init__(self, a, dim, size):
input_shape = a.shape[:]
assert input_shape[dim] == 1, f"Input tensor must have size 1 in dimension {dim}"
input_shape[dim] = size
super().__init__(shape=input_shape)
self.a = a
self.dim = dim
self.size = size
self.dependencies = [a]
def _materialize(self):
ma = self.a.materialize()
result = Tensor(self.shape)
for i in range(self.size): # Clone the tensor N times
ctypes.memmove(result.data.ctypes.data + i * ma.data.nbytes, ma.data.ctypes.data, ma.data.nbytes)
return result
def _backward(self):
# Reduce the gradient
N = self.size
for i in range(N):
self.a.grad.data = self.a.grad.data + self.grad.data[i * len(self.a.grad.data):(i + 1) * len(self.a.grad.data)]
class AdamW:
"""
Simple AdamW without variance bias correction
"""
def __init__(self, parameters, lr=0.001, betas=(0.9, 0.999), weight_decay=0.01):
self.parameters = parameters
self.lr = lr
self.betas = betas
self.weight_decay = weight_decay
self.moments_1 = []
self.moments_2 = []
for p in parameters:
self.moments_1.append(Tensor(p.grad.shape))
self.moments_2.append(Tensor(p.grad.shape))
def step(self):
for i, p in enumerate(self.parameters):
self.moments_1[i] = self.moments_1[i] * self.betas[0] + p.grad * (1 - self.betas[0])
self.moments_2[i] = self.moments_2[i] * self.betas[1] + (p.grad * p.grad) * (1 - self.betas[1])
variance = self.moments_2[i] - self.moments_1[i] * self.moments_1[i]
p.values.data -= self.lr * self.moments_1[i].data / (np.sqrt(self.moments_2[i].data) + 1e-8)
p.values.data -= self.weight_decay * self.lr * p.values.data
if 0:
a = LearnableParameter(shape=[1, 3])
b = LearnableParameter(shape=[1, 3])
m0 = Matrix(in_channels=3, out_features=3)
adamw = AdamW(parameters=[a, b, m0], lr=0.01333, weight_decay=0.0, betas=(0.9, 0.999))
for epoch in range(3000):
x = Variable(Tensor(shape=[1, 3], data=[[random.random(), random.random(), random.random()]]), name="x")
y = VectorMatrixMultiply(Square(x), m0) + b
loss = Reduce(Square(y - (Square(x) * Constant(Tensor(shape=[1, 3], data=[[1.777, 1.333, 0.333]])) + Constant(Tensor(shape=[1, 3], data=[[1.55, 0.0, -1.666]]))))) # L2 loss to Ax^2+B
print(f"Epoch {epoch}: loss = {loss.materialize().data[0]}; a = {a.materialize().data}, b = {b.materialize().data}, \nm0 = \n{m0.materialize().data.reshape(3, 3)}")
# Backward pass
# Gradient reset happens internally in the backward pass
loss.backward()
adamw.step()
exit()
num_input_features = 64
num_nodes = 64
batch_size = 64
num_epochs = 32000
m0 = Matrix(in_channels=num_input_features, out_features=num_nodes)
b0 = LearnableParameter(shape=[1, num_nodes,]) # bias
m1 = Matrix(in_channels=num_nodes, out_features=num_nodes)
b1 = LearnableParameter(shape=[1, num_nodes,]) # bias
m2 = Matrix(in_channels=num_nodes, out_features=num_nodes)
b2 = LearnableParameter(shape=[1, num_nodes]) # bias
m3 = Matrix(in_channels=num_nodes, out_features=3)
b3 = LearnableParameter(shape=[1, 3]) # bias
def broadcast_to_batch(node, batch_size):
return Broadcast(node, dim=0, size=batch_size)
def broadcast_rgb_mul(k, batch_size):
n = np.zeros((batch_size, 3), dtype=np.float32)
n[:, 0] = k
n[:, 1] = k
n[:, 2] = k
return n
def eval_mlp(x):
batch_size = x.shape[0]
z = VectorMatrixMultiply(tensor=x, matrix=m0)
z = z + broadcast_to_batch(b0, batch_size)
z = LeakyRelu(z, negative_slope=0.1)
z = VectorMatrixMultiply(tensor=z, matrix=m1)
z = z + broadcast_to_batch(b1, batch_size)
z = LeakyRelu(z, negative_slope=0.1)
z = VectorMatrixMultiply(tensor=z, matrix=m2)
z = z + broadcast_to_batch(b2, batch_size)
z = LeakyRelu(z, negative_slope=0.1)
z = VectorMatrixMultiply(tensor=z, matrix=m3)
# z = z + broadcast_to_batch(b3, batch_size)
# z = LeakyRelu(z, negative_slope=0.01)
return z
def eval_target(x):
return x * x * 2.777 + 0.624 - x * x * x * 0.333 + np.sin(x * 5.0) * 0.777
adamw = AdamW(parameters=[m0, b0, m1, b1, m2, b2, m3, b3], lr=0.000533, weight_decay=0.01, betas=(0.92, 0.95))
import matplotlib.image as image
ref = image.imread("mlp_compression/assets/mandrill.png")
print(f"Reference image shape: {ref.shape}")
# Initialize all the feature vectors for every pixel on the image
size = 512
x_data = np.zeros((size, size, num_input_features), dtype=np.float32)
print(f"Initializing the grid...")
# for pixel_x in range(size):
# for pixel_y in range(size):
# # Frequency encoding
# for i in range(num_input_features // 4):
# x_data[pixel_x, pixel_y, i * 4 + 0] = math.sin(pixel_x * (2.0 ** (i + 1)) * math.pi / size)
# x_data[pixel_x, pixel_y, i * 4 + 1] = math.cos(pixel_x * (2.0 ** (i + 1)) * math.pi / size)
# x_data[pixel_x, pixel_y, i * 4 + 2] = math.sin(pixel_y * (2.0 ** (i + 1)) * math.pi / size)
# x_data[pixel_x, pixel_y, i * 4 + 3] = math.cos(pixel_y * (2.0 ** (i + 1)) * math.pi / size)
L = num_input_features // 4
xx, yy = np.meshgrid(np.arange(size), np.arange(size))
freqs = (2.0 ** (np.arange(L) + 1)) * np.pi / size
x_sin = np.sin(yy[:, :, None] * freqs[None, None, :])
x_cos = np.cos(yy[:, :, None] * freqs[None, None, :])
y_sin = np.sin(xx[:, :, None] * freqs[None, None, :])
y_cos = np.cos(xx[:, :, None] * freqs[None, None, :])
stacked = np.stack([x_sin, x_cos, y_sin, y_cos], axis=-1)
x_data[:] = stacked.reshape(size, size, -1)
for epoch in range(num_epochs):
_x_data = np.zeros((batch_size, num_input_features), dtype=np.float32)
y_data = np.zeros((batch_size, 3), dtype=np.float32)
for b in range(batch_size):
pixel_x = int(random.random() * ref.shape[0])
pixel_y = int(random.random() * ref.shape[1])
_x_data[b] = x_data[pixel_x, pixel_y]
y_data[b, 0] = ref[pixel_x, pixel_y, 0]
y_data[b, 1] = ref[pixel_x, pixel_y, 1]
y_data[b, 2] = ref[pixel_x, pixel_y, 2]
x = Variable(Tensor(shape=[batch_size, num_input_features], data=_x_data), name="x")
mlp = eval_mlp(x)
loss = Reduce(Square(mlp - Constant(Tensor(shape=[batch_size, 3], data=y_data))) +
Exp(Abs(mlp - Constant(Tensor(shape=[batch_size, 3], data=y_data)))) * Constant(Tensor(shape=[batch_size, 3], data=broadcast_rgb_mul(0.25, batch_size))), op='+')
if epoch == 0:
with open(".tmp/graph.dot", "w") as f:
f.write(loss.pretty_print_dot_graph())
print(f"Epoch {epoch}: loss = {loss.materialize().data[0] / batch_size}; lr = {adamw.lr}")
# Backward pass
# Gradient reset happens internally in the backward pass
loss.backward()
adamw.step()
adamw.lr *= 0.99999
# Plot our mlp
import matplotlib.pyplot as plt
# render the image
x = Variable(Tensor(shape=[size * size, num_input_features], data=x_data), name="x")
y_data = eval_mlp(x).materialize().data.reshape((size, size, 3))
plt.imshow(y_data, aspect="auto")
plt.axis("off")
plt.show()
Links
[1]You could have designed state of the art positional encoding